Satz des Pythagoras
Aus MosaPedia
(→Bei den Digedags) |
Bhur (Diskussion | Beiträge) K (→Bei den Abrafaxen) |
||
| (Der Versionsvergleich bezieht 17 dazwischenliegende Versionen mit ein.) | |||
| Zeile 1: | Zeile 1: | ||
[[Bild:SatzPythagoras.jpg|right|frame|[[Brabax]] studiert den Satz des [[Pythagoras]]]] | [[Bild:SatzPythagoras.jpg|right|frame|[[Brabax]] studiert den Satz des [[Pythagoras]]]] | ||
Der '''Satz des Pythagoras''' kommt mehrfach im [[MOSAIK]] und auch in einem [[Nebenuniversum]] vor. | Der '''Satz des Pythagoras''' kommt mehrfach im [[MOSAIK]] und auch in einem [[Nebenuniversum]] vor. | ||
| - | Der geometrische Satz | + | Der geometrische Satz, den viele als die Formel ''a²+b²=c²'' kennen, der die Seitenverhältnisse eines rechtwinkligen Dreiecks beschreibt, wird [[Pythagoras]] (* um 570 v. Chr., † nach 510 v. Chr.) zugeschrieben. In der Gleichung sind ''a'' und ''b'' die Längen der am rechten Winkel anliegenden Seiten, der beiden Katheten. Die Hypotenuse ''c'' liegt dem rechten Winkel gegenüber. |
=== Bei den [[Digedags]] === | === Bei den [[Digedags]] === | ||
| Zeile 7: | Zeile 7: | ||
Auf dem [[Nucleon]] finden die Digedags das [[wissenschaftliches Testament von Professor Ingstorn|wissenschaftliche Testament]] von [[Professor Ingstorn]]. Darin erwähnt er eine Erfindung, die zum Segen seines Planeten verwendet werden soll. Er hat sie jedoch verschlüsselt und [[Sinus Tangentus]] erkennt darin eine geometrische Aufgabe. Hier ist der Wortlaut: | Auf dem [[Nucleon]] finden die Digedags das [[wissenschaftliches Testament von Professor Ingstorn|wissenschaftliche Testament]] von [[Professor Ingstorn]]. Darin erwähnt er eine Erfindung, die zum Segen seines Planeten verwendet werden soll. Er hat sie jedoch verschlüsselt und [[Sinus Tangentus]] erkennt darin eine geometrische Aufgabe. Hier ist der Wortlaut: | ||
{{Zitat| | {{Zitat| | ||
| - | Von Süden bis nach Norden geh,<br>das Planetarium und das Kreuz sind B und C.<br>Von C geh ostwärts bis nach A,<br>der Drei, Vier, Fünf gedenke da.<br>Des Kreises Zentrum dich zum Ziele führt,<br>der mit den Seiten a, b, c tangiert.}} | + | Von Süden bis nach Norden geh,<br>das [[Planetarium]] und das Kreuz sind B und C.<br>Von C geh ostwärts bis nach A,<br>der Drei, Vier, Fünf gedenke da.<br>Des Kreises Zentrum dich zum Ziele führt,<br>der mit den Seiten a, b, c tangiert.}} |
| - | Mit Hilfe eines [[Stadtplan]]s und des Lehrsatzes des Pythagoras kann Sinus Tangentus das Rätsel lösen. Drei, Vier und Fünf | + | Mit Hilfe eines [[Stadtplan]]s und des Lehrsatzes des Pythagoras kann Sinus Tangentus das Rätsel lösen. Die leicht merkbaren Zahlen Drei, Vier und Fünf bilden das kleinste und bekannteste ''pythagoreische Tripel'', d.h. das kleinste ''ganzzahlige'' Verhältnis der Seiten eines rechtwinkligen Dreiecks. |
{{Zitat| | {{Zitat| | ||
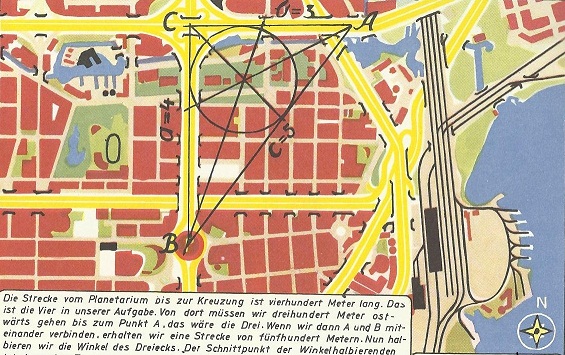
| - | Die Strecke vom Planetarium bis zur Kreuzung ist vierhundert Meter lang. Das ist die Vier in unserer Aufgabe. Von dort aus müssen wir dreihundert Meter ostwärts gehen | + | Die Strecke vom Planetarium bis zur Kreuzung ist vierhundert Meter lang. Das ist die Vier in unserer Aufgabe. Von dort aus müssen wir dreihundert Meter ostwärts gehen bis zum Punkt A, das wäre die Drei. Wenn wir dann A und B miteinander verbinden, erhalten wir eine Strecke von fünfhundert Metern. Nun halbieren wir die Winkel des Dreiecks. Der Schnittpunkt der Winkelhalbierenden ist dann das Zentrum des Innenkreises, der die Seiten a - b - c berührt.}} |
| - | + | Nachdem mit Hilfe des [[Satz über die Winkelhalbierenden im Dreieck|Satzes über Inkreis und Winkelhalbierende]] der Zielort des Rätsels auf dem Stadtplan bestimmt ist, begeben sie sich dorthin und treffen auf die [[Villa von Professor Ingstorn]], in der sich die gesuchte Erfindung, eine [[künstliche Sonne]], befindet. | |
<br clear=both> | <br clear=both> | ||
=== Bei den [[Abrafaxe]]n === | === Bei den [[Abrafaxe]]n === | ||
| - | Auf Seite 3 von Heft [[1/76]] studiert Brabax offensichtlich gerade | + | Auf Seite 3 von Heft [[1/76]] [[Brabax als Wissenschaftler|studiert Brabax]] offensichtlich gerade [[Euklid]]s Werke. Auf der linken Seite des aufgeschlagenen Buches ist eine graphische Darstellung des Satzes des Pythagoras erkennbar. Auf der gegenüberliegenden Seite findet sich eine Illustration zum ''Kathetensatz des Euklid''. Letzterer Satz, der die Aufteilung des Hypotenusenquadrates in zwei Rechtecke berschreibt und dessen Aussage häufig mit den kurzen Formeln ''a²=p·c'', ''b²=q·c'' wiedergegeben wird, findet sich quasi als "Zwischenergebnis" in Euklids Beweis zum Satz des Pythagoras (''Elemente'' I 47). |
| + | (Bei Brabax' Buch handelt es sich aber offensichtlich um Sekundärliteratur: die Zeichnungen sind nicht den ''Elementen'' Euklids entnommen). | ||
| - | Als Wortspiel findet sich Pythagoras' Satz auch auf Seite 10 des Heftes [[4/84]]. Alexander Papatentos | + | Als Wortspiel findet sich Pythagoras' Satz auch auf Seite 10 des Heftes [[4/84]] der [[Alexander-Papatentos-Serie]]. [[Alexander Papatentos|Alex]] bemerkt, dass die Abrafaxe von ihm aus soviele "Hypothenusen" aufstellen könnten wie der alte Pythagoras. Er verwechselt hier Hypothese und Hypotenuse. Brabax wollte eine Hypothese zum Verbleib des [[Schild des Königs Poros|Schilds des Poros]] aufstellen. Für den berühmten Satz des Pythagoras dagegen ist die Hypotenuse von Bedeutung, die dem rechten Winkel gegenüberliegende Seite eines rechtwinkligen Dreiecks. |
| + | |||
| + | In der [[Ozeanien-Serie]] erfährt Brabax, dass [[Califax]] und [[Pitipak]] gerade zurückgekehrt sind. Erleichtert ruft er: "Beim Satz des Pythagoras - bin ich froh!" | ||
=== Im [[Nebenuniversum]] === | === Im [[Nebenuniversum]] === | ||
*Im Onepager ''[[Onepager SI 327 - Scherbengericht|Scherbengericht]]'' hat Brabax am Kaffeetisch ein Buch mit dem Satz des Pythagoras aufgeschlagen. | *Im Onepager ''[[Onepager SI 327 - Scherbengericht|Scherbengericht]]'' hat Brabax am Kaffeetisch ein Buch mit dem Satz des Pythagoras aufgeschlagen. | ||
| - | == | + | == Externe Links == |
| - | *Der [http://de.wikipedia.org/wiki/Satz_des_Pythagoras Satz des Pythagoras] in der [[Wikipedia]] | + | * Der [http://de.wikipedia.org/wiki/Satz_des_Pythagoras Satz des Pythagoras] in der [[Wikipedia]] |
| + | * Daselbst: [http://de.wikipedia.org/wiki/Pythagoreisches_Tripel Pythagoreisches Tripel], [http://de.wikipedia.org/wiki/Kathetensatz Kathetensatz] | ||
| + | * Euklids [http://www.opera-platonis.de/euklid/Buch1.pdf Elemente, Buch I], hier: I.47. | ||
== Der Satz des Pythagoras kommt in folgenden MOSAIK-Publikationen vor == | == Der Satz des Pythagoras kommt in folgenden MOSAIK-Publikationen vor == | ||
[[Mosaik von Hannes Hegen]]: [[27]] | [[Mosaik von Hannes Hegen]]: [[27]] | ||
| - | [[Mosaik ab 1976]]: [[1/76]], [[4/84]] | + | [[Mosaik ab 1976]]: [[1/76]], [[4/84]], [[534]] |
[[Onepager]]: [[Onepager SI 327 - Scherbengericht]] | [[Onepager]]: [[Onepager SI 327 - Scherbengericht]] | ||
| Zeile 36: | Zeile 41: | ||
[[Kategorie:Adria-Serie (Ereignis)]] | [[Kategorie:Adria-Serie (Ereignis)]] | ||
[[Kategorie:Alexander-Papatentos-Serie (Ereignis)]] | [[Kategorie:Alexander-Papatentos-Serie (Ereignis)]] | ||
| + | [[Kategorie:Ozeanien-Serie (Ereignis)]] | ||
[[Kategorie:Abrafaxe in der Super Illu (Ereignis)]] | [[Kategorie:Abrafaxe in der Super Illu (Ereignis)]] | ||
Aktuelle Version vom 16:38, 20. Jun. 2020

Der Satz des Pythagoras kommt mehrfach im MOSAIK und auch in einem Nebenuniversum vor. Der geometrische Satz, den viele als die Formel a²+b²=c² kennen, der die Seitenverhältnisse eines rechtwinkligen Dreiecks beschreibt, wird Pythagoras (* um 570 v. Chr., † nach 510 v. Chr.) zugeschrieben. In der Gleichung sind a und b die Längen der am rechten Winkel anliegenden Seiten, der beiden Katheten. Die Hypotenuse c liegt dem rechten Winkel gegenüber.
Inhaltsverzeichnis |
[Bearbeiten] Bei den Digedags
Auf dem Nucleon finden die Digedags das wissenschaftliche Testament von Professor Ingstorn. Darin erwähnt er eine Erfindung, die zum Segen seines Planeten verwendet werden soll. Er hat sie jedoch verschlüsselt und Sinus Tangentus erkennt darin eine geometrische Aufgabe. Hier ist der Wortlaut:
|
Von Süden bis nach Norden geh, |
Mit Hilfe eines Stadtplans und des Lehrsatzes des Pythagoras kann Sinus Tangentus das Rätsel lösen. Die leicht merkbaren Zahlen Drei, Vier und Fünf bilden das kleinste und bekannteste pythagoreische Tripel, d.h. das kleinste ganzzahlige Verhältnis der Seiten eines rechtwinkligen Dreiecks.
|
Die Strecke vom Planetarium bis zur Kreuzung ist vierhundert Meter lang. Das ist die Vier in unserer Aufgabe. Von dort aus müssen wir dreihundert Meter ostwärts gehen bis zum Punkt A, das wäre die Drei. Wenn wir dann A und B miteinander verbinden, erhalten wir eine Strecke von fünfhundert Metern. Nun halbieren wir die Winkel des Dreiecks. Der Schnittpunkt der Winkelhalbierenden ist dann das Zentrum des Innenkreises, der die Seiten a - b - c berührt. |
Nachdem mit Hilfe des Satzes über Inkreis und Winkelhalbierende der Zielort des Rätsels auf dem Stadtplan bestimmt ist, begeben sie sich dorthin und treffen auf die Villa von Professor Ingstorn, in der sich die gesuchte Erfindung, eine künstliche Sonne, befindet.
[Bearbeiten] Bei den Abrafaxen
Auf Seite 3 von Heft 1/76 studiert Brabax offensichtlich gerade Euklids Werke. Auf der linken Seite des aufgeschlagenen Buches ist eine graphische Darstellung des Satzes des Pythagoras erkennbar. Auf der gegenüberliegenden Seite findet sich eine Illustration zum Kathetensatz des Euklid. Letzterer Satz, der die Aufteilung des Hypotenusenquadrates in zwei Rechtecke berschreibt und dessen Aussage häufig mit den kurzen Formeln a²=p·c, b²=q·c wiedergegeben wird, findet sich quasi als "Zwischenergebnis" in Euklids Beweis zum Satz des Pythagoras (Elemente I 47). (Bei Brabax' Buch handelt es sich aber offensichtlich um Sekundärliteratur: die Zeichnungen sind nicht den Elementen Euklids entnommen).
Als Wortspiel findet sich Pythagoras' Satz auch auf Seite 10 des Heftes 4/84 der Alexander-Papatentos-Serie. Alex bemerkt, dass die Abrafaxe von ihm aus soviele "Hypothenusen" aufstellen könnten wie der alte Pythagoras. Er verwechselt hier Hypothese und Hypotenuse. Brabax wollte eine Hypothese zum Verbleib des Schilds des Poros aufstellen. Für den berühmten Satz des Pythagoras dagegen ist die Hypotenuse von Bedeutung, die dem rechten Winkel gegenüberliegende Seite eines rechtwinkligen Dreiecks.
In der Ozeanien-Serie erfährt Brabax, dass Califax und Pitipak gerade zurückgekehrt sind. Erleichtert ruft er: "Beim Satz des Pythagoras - bin ich froh!"
[Bearbeiten] Im Nebenuniversum
- Im Onepager Scherbengericht hat Brabax am Kaffeetisch ein Buch mit dem Satz des Pythagoras aufgeschlagen.
[Bearbeiten] Externe Links
- Der Satz des Pythagoras in der Wikipedia
- Daselbst: Pythagoreisches Tripel, Kathetensatz
- Euklids Elemente, Buch I, hier: I.47.
[Bearbeiten] Der Satz des Pythagoras kommt in folgenden MOSAIK-Publikationen vor
Mosaik von Hannes Hegen: 27 Mosaik ab 1976: 1/76, 4/84, 534 Onepager: Onepager SI 327 - Scherbengericht