Satz über die Winkelhalbierenden im Dreieck
Aus MosaPedia
Kobold (Diskussion | Beiträge) (→Externe Links: +3) |
Kobold (Diskussion | Beiträge) (→Winkelhalbierende und Inkreis bei den Digedags: Bemerkenswert...klarer) |
||
| Zeile 20: | Zeile 20: | ||
* Der Inkreis als solcher ist im Testament unverschlüsselt benannt. Der gesuchte Ort im Zentrum – die [[Villa von Professor Ingstorn|Villa Ingstorns]] – kann nun mit Hilfe des Satzes über die Winkelhalbierenden genau bestimmt werden. | * Der Inkreis als solcher ist im Testament unverschlüsselt benannt. Der gesuchte Ort im Zentrum – die [[Villa von Professor Ingstorn|Villa Ingstorns]] – kann nun mit Hilfe des Satzes über die Winkelhalbierenden genau bestimmt werden. | ||
| - | Bemerkenswert ist, dass der | + | Bemerkenswert ist, dass der Satz über die Winkelhalbierenden nicht nur zielführend angewendet, sondern auch in der Handlung erklärt und im Comic-Panel anschaulich illustriert wird: |
| + | Für die Bestimmung des gesuchten Kreismittelpunktes im Stadtplan wären eigentlich zwei der drei Winkelhalbierenden ausreichend (wer sich selbst nicht über den Weg traut, ''kann'' die dritte zur Kontrolle einzeichnen). Indem Sinus Tangentus aber die Zeichnung vervollständigt und auch noch den im Rätsel genannten Kreis hinzufügt, zeigt er seinen Begleitern und damit auch dem Leser: Seht her! So geht das, und es funktioniert! – In dieser Form ist die Präsentation des geometrischen Satzes wohl einmalig in der Mosaik-Welt, ein [[Brabax]] gibt sich bei seinen Geniestreichen um einiges wortkarger. | ||
<br style="clear:both" /> | <br style="clear:both" /> | ||
Version vom 00:03, 18. Feb. 2015
In der Weltraum-Serie des Mosaik von Hannes Hegen wird ein bekannter Satz aus der Geometrie über die Winkelhalbierenden im Dreieck zitiert und illustriert. Dieser besagt zweierlei:
- Die drei Winkelhalbierenden eines Dreiecks schneiden sich in einem Punkt, und
- dieser Punkt ist zugleich der Mittelpunkt des Inkreises (d.h. des Kreises, der alle drei Dreiecksseiten von innen berührt).
Winkelhalbierende und Inkreis bei den Digedags
In der Hauptstadt des verwüsteten Planeten Nucleon sind die Digedags auf der Suche nach dem Ort, an dem der Atomforscher Professor Ingstorn eine bedeutende Erfindung versteckt hat. Das wisenschaftliche Testament des Forschers enthält dazu ein Rätsel in Reimform:
|
Von Süden bis nach Norden geh, |
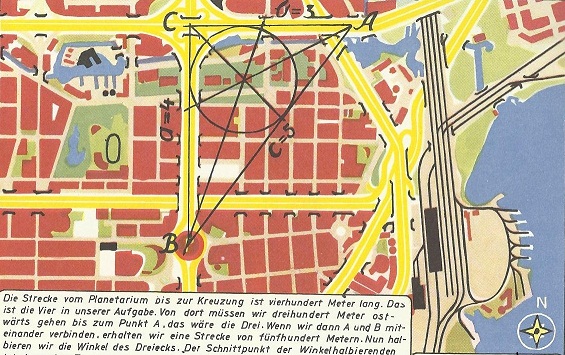
Mit Hilfe eines Stadtplans und seiner Kenntnisse der Mathematik ist es für Sinus Tangentus kein Problem, diese "antike" Form einer Geocaching-Aufgabe zu lösen. Er erklärt dazu:
|
Die Strecke vom Planetarium bis zur Kreuzung ist vierhundert Meter lang. Das ist die Vier in unserer Aufgabe. Von dort aus müssen wir dreihundert Meter ostwärts gehen bis zum Punkt A, das wäre die Drei. Wenn wir dann A und B miteinander verbinden, erhalten wir eine Strecke von fünfhundert Metern. Nun halbieren wir die Winkel des Dreiecks. Der Schnittpunkt der Winkelhalbierenden ist dann das Zentrum des Innenkreises, der die Seiten a - b - c berührt. |
Aus mathematischer Sicht besteht die Aufgabe aus zwei Teilen:
- Die scheinbar zusammenhanglos in den Vers eingestreuten Zahlen erinnern an das (kleinste und bekannteste) pythagoreische Tripel 3:4:5, das hier offensichtlich als Seitenverhältnis eines rechtwinkligen Dreiecks aufzufassen ist. Nun müssen die Seiten richtig zugeordnet werden: 3:4 oder 4:3? Dabei kommt Sinus Tangentus entgegen, dass auf dem Nucleon ebenso wie in Kontinentaleuropa in Metern gemessen wird (und nicht etwa in Yard oder Meilen). Bis hierhin eher eine detektivische Aufgabe...
- Der Inkreis als solcher ist im Testament unverschlüsselt benannt. Der gesuchte Ort im Zentrum – die Villa Ingstorns – kann nun mit Hilfe des Satzes über die Winkelhalbierenden genau bestimmt werden.
Bemerkenswert ist, dass der Satz über die Winkelhalbierenden nicht nur zielführend angewendet, sondern auch in der Handlung erklärt und im Comic-Panel anschaulich illustriert wird: Für die Bestimmung des gesuchten Kreismittelpunktes im Stadtplan wären eigentlich zwei der drei Winkelhalbierenden ausreichend (wer sich selbst nicht über den Weg traut, kann die dritte zur Kontrolle einzeichnen). Indem Sinus Tangentus aber die Zeichnung vervollständigt und auch noch den im Rätsel genannten Kreis hinzufügt, zeigt er seinen Begleitern und damit auch dem Leser: Seht her! So geht das, und es funktioniert! – In dieser Form ist die Präsentation des geometrischen Satzes wohl einmalig in der Mosaik-Welt, ein Brabax gibt sich bei seinen Geniestreichen um einiges wortkarger.
Externe Links
- Wikipedia: Winkelhalbierende und Inkreis im Dreieck
- Incircle auf wolfram.com (englisch)
Der Satz wird in folgendem Mosaikheft zitiert
27